The AECOM13 study has a detailed cost breakdown for various types of earthworks, a simplified version of which will be adopted for Hot Rails.
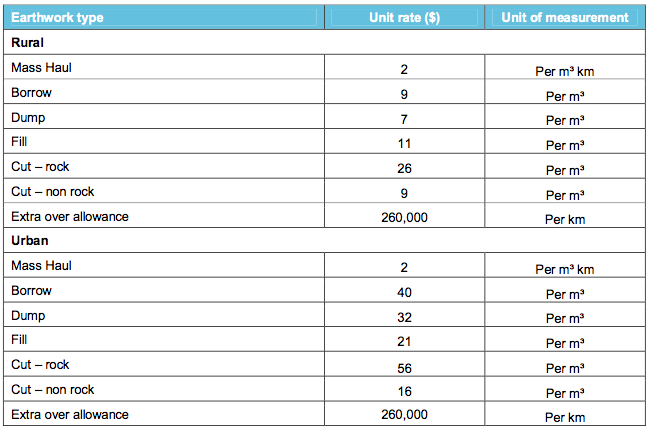
Indicative capital cost estimates – HSR earthworks, rural and urban. Source: AECOM13, Appendix 4B pg. 9
First, some definitions:
“Cut” is your basic excavation – there is dirt or rock in your way, and you want it not to be there. “Fill” is the opposite – the ground is lower than where you want it to be, and you dump dirt or rock to raise it.
If your cut doesn’t equal your fill, you need to make it equal. If you need more fill than you have cut, you need to dig extra fill, called “borrow”, usually by digging a borrow pit nearby. If your cuts generate more fill than you need, the excess fill needs to be deposited somewhere, most commonly just a big pile somewhere unobtrusive – this is “dump”.
“Mass haul” means trucking fill from here to there. Careful alignment design seeks to balance the amount of cut and fill, and also minimise the distance between cut and fill sites.
“Extra over allowance” is defined as “allowance for additional sundry works and known unknowns”. The cost “per km” presumably means per kilometre of earthworks, not per kilometre of railway, although this is unclear.
The economics of mass-haul
How far can you haul a load of fill before it becomes more economic just to dump it? Or alternatively, how far away can you look for extra fill before it becomes more economic to borrow it?
Consider a hypothetical rural earthworks which consists of a 1000m3 cut (rock). The cost to cut-and-dump is ($26 × 1000) + ($7 × 1000) = $33,000. Now suppose that nearby there is a fill of 1000m3. The cost of borrow-and-fill is ($11 × 1000) + ($9 × 1000) = $19,000, or a total of $52,000 for both the cut and the fill. But if we consider the cut-and-fill together, we see that they are balanced – the material excavated from the cut can provide all the material for the fill, eliminating the need to dump or borrow. Now the cost of the cut-and-fill is: ($26 × 1000) + ($11 × 1000) + ($2 × 1000 × distance). With the cut/fill costing $37,000, and the borrow/dump $15,000, the balanced cut/fill will be cheaper than the individual cut/fill up to a haul distance of 7.5km.
It is desirable to avoid borrow and dump even at moderate extra haulage cost, due to the added environmental impact caused. The question is how accurately do we want to estimate this, since we won’t have access to sophisticated alignment estimation software. Perhaps a reasonable approximation would be to assume a certain distance of haulage in the cost of cut and fill. If we assume that each unit of hauled mass represents both a cut and a fill, then every additional $1/m3 is equivalent to including an additional 1km haul in the cost estimate. If we include a haul distance of 5km in the cost of the cut and fill, we can assume all balanced cut-and-fill in a particular analysis sector (generally under 10km) to have haulage priced-in; any unbalanced excavation will be hauled from (or to) elsewhere at $2/m3-km.
Typical sections
I figure that as far as determining the typical cross section of a railway goes, the old ways are most probably just as good if not better than the new. After all, the lines they built back then are still standing for the most part. The above image from the 1902 Encyclopaedia Britannica shows a typical cross section of the British National Gauge (ie, railway standards). In gravel, sand or earth, the slope is commonly limited to 1½ to 1 (33.7°). In rock, the slope can be almost vertical.
The slope isn’t always going to be 1½ to 1 of course, although this is what we’ll assume for soft ground. Wikipedia has a list of angles of repose for various materials, ie, the angle relative to the horizontal at which a pile of said material will sit without slumping. Most building materials (sand, gravel, earth, etc) have an angle of repose of 30°-45°, so 1½ to 1 is a conservative estimate for most situations. However, much of the alignment will be through rock, where the angle can be much steeper. Now I have no time, interest or ability to go out and do geological studies at each earthwork site to determine the ideal slope angle. Sometimes it will be flatter than 45°, sometimes it will be steeper. In this study we will assume a constant cut angle of 45° in order to make calculation simpler.
AECOM13 assumes the width of the dual-track to be 11.3m between centres of the OHLE support poles. A 12m base width for each cutting or embankment is therefore a conservative estimate. This is confirmed by analysis of the existing Sydney-Melbourne line using Google Earth imagery, but should also be confirmed by on-site measurement when possible.
Estimating volume
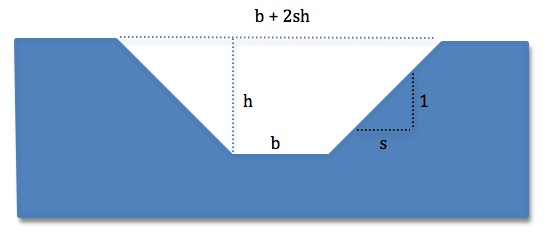
We want to be able to estimate cut or fill volume as a function of height. The shape of a cut or a fill can be approximated as a trapezoidal prism. The area of a trapezoid is the average of the wide and narrow ends, multiplied by the height. So if we assume a typical cut has a slope of 1½ to 1, and the narrow end is 12m wide, the wide end will be 12m + 2×(1.5h). The average of this is therefore 12+1.5h, and so the area, in square metres, is 12h+1.5h2. Multiply by the length of the cut in metres to find the volume.
More generally, for a cut with a base width b, height h and slope s (where slope = s to 1), the section area is bh+sh2.
This assumes that the excavation will be uniform in depth, which is obviously a simplification. Elevation profiles will be used to visually estimate the average depth of the cut or fill, and calculate the volume as if the depth were constant. Although this will tend to slightly under-estimate volume, the error is small enough to be ignored. Detailed corridor analysis with specialised software would be used to confirm accurate volumes at a later date.
Widening an existing cutting or embankment requires much less volume; the volume is simply the extra width multiplied by the height.
Volumetric cost
We use the AECOM13 assumptions but with 5km of mass-haul assumed as part of the base cost. Given the example section above, where it is evident that most excavation can be balanced well within 5km (typically under 2km), this builds in significant contingency to the estimate.
- Rural:
- Cut (rock): $31/m3
- Cut (non-rock): $14/m3
- Fill: $16/m3
- Urban:
- Cut (rock): $61/m3
- Cut (non-rock): $21/m3
- Fill: $26/m3
Any excess must be hauled away to somewhere with a deficit – cost this at $2/m3-kg over and above the 5km assumed, making sure not to double-count. We will generally try to avoid borrowing or dumping.
Typical values
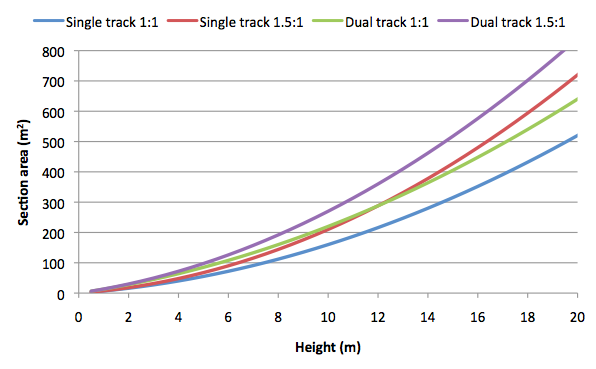
The following graph shows the relationship of cut cost to cut depth for several situations. To convert this to a per-metre cost, multiply by the type of earthwork performed (ie rock cut, non-rock cut, fill, urban or rural). For example, a 5-metre cutting in rock for rural dual-track at 1:1 would cost 74m2×1000m×$31 = $2.29m/km.
Cuts vs Tunnels
At some point, it becomes more economic to build a tunnel rather than dig a deeper cut. Often this is the case in quite shallow alignments due to the expense of acquiring surface land, such as in suburban or inner-city areas. AECOM13 mentions in passing that even in rural areas, deep cuttings up to 50 metres in depth may be economically preferable to tunnels in some situations. Have you ever seen a 50 metre deep cutting? This is yet more evidence that the estimate for tunnels is vastly overstated in AECOM13, but let’s put it to the test anyway. A 50 metre deep, 1.5:1 slope, rural rock cutting costs $134.9m/km, which is indeed less than the $147.6m/km AECOM13 assumes for a twin-bore tunnel.
What about Hot Rails? Using our assumptions, at what depth does it become more economic to tunnel? Assuming $75m/km for dual-bore 300km/h tunnel, rural 1.5:1 rock cut becomes more expensive at a depth of 36m; for 1:1 cut it is about 44m. For the purposes of the Hot Rails study, we will assume any cut deeper than 40m should definitely be replaced by a tunnel.
Between 20 and 40m, it becomes highly dependent on other costs avoided by tunnelling, principally real estate. The cost of land acquisition starts becoming a significant cost (more than $1m/km) where the landuse begins to change from hobby farms to minor town residential areas (also keeping in mind that a wider corridor is required where cuts or fills are used). In these areas the cost of tunnels may be justified at much shallower depths.