One of the primary cost drivers of high-speed rail is the fact that the track must be far straighter and flatter than standard rail lines. In order to achieve this, far more earthworks, bridges and tunnels are required, which are extremely expensive. Hot Rails aims to use tilting trains to achieve high speeds with shorter radii. But how do we determine the minimum allowed radius of our railway, and just how much smaller can tilt trains allow the radius to be?
Horizontal alignment
The permissable speed for a standard-gauge railway alignment is governed by the following equation:
![]()
where:
V = permissible speed (km/h)
R = radius of horizontal curvature (m)
Ilim = permissible cant deficiency (mm)
Dlim = permissible cant (mm)
11.8 = factor applicable for standard gauge 1435mm
Cant or superelevation is the difference in height between the inside and the outside rail. Positive cant assists cornering by directing a portion of the normal force in the radial direction, reducing the amount of friction required to turn the vehicle. Cant deficiency is defined as the amount by which the outside rail would have to be raised, such that a train travelling at design speed could traverse the curve with no friction. The denominator, 11.8, is a factor dependent on the width (gauge) of the railway.
Curve radius
It is apparent that in order to minimise R, we wish to maximise the sum of cant and cant deficiency. Cant is set when the railway is constructed; its value is limited by the fact that trains must be able to safely stop on the banked curve without toppling over. Australian design guidelines call for a typical limit of 150mm cant and 110mm cant deficiency for lines used by XPT type passenger trains. In order to achieve our required design speed of 200km/h, this necessitates a curve radius of 1815m – much larger than the existing minimum on most Australian railways, and impractically large for the strategy outlined in this blog. We need to find a way to increase Ilim +Dlim.
Tilting trains can achieve this without dangerously high levels of cant, as they can operate at higher levels of cant deficiency. Their ability to lean into the turn shifts the train’s centre of gravity, compensating for the unbalanced centrifugal force.
The following table shows various standards for cant and cant deficiency in several areas around the world, as well as moderate and aggressive tilt. It also shows the required radius for our chosen design speed of 200km/h.
[table]
,Australia (XPT),Italy,UK and Germany,France (TGV),Tilt Trains Low,Tilt Trains High
Cant (mm),150,160,180,180,150,200
Cant Deficiency (mm),110,122,150,180,250,300
R for 200km/h (m),1815,1674,1430,1311,1180,944
[/table]
The speed/radius relationship is plotted below; it agrees closely with the graph on page 29 of ARUP01.
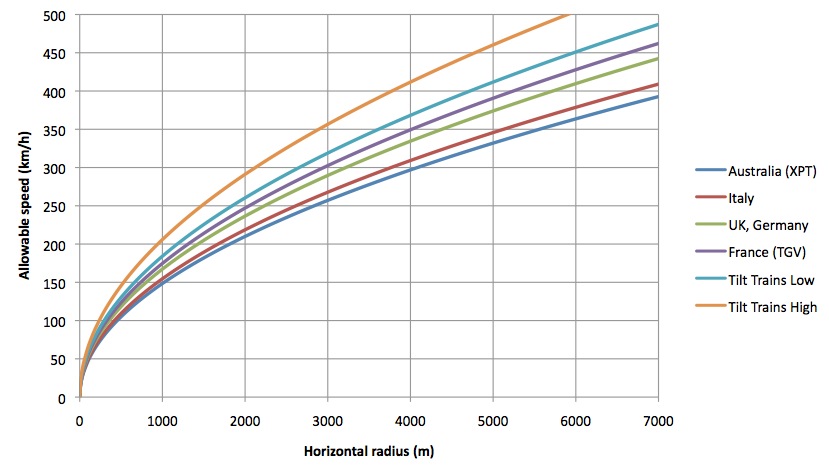 If Australia were to adopt a tilt train standard of D=180mm and I=300mm, this would allow a minimum radius of 983m at the design speed of 200km/h. Although this is a relatively aggressive tilt, it is the same as that used by both the UK and Germany. Modern tilt systems which anticipate curves in the track automatically are able to almost completely eliminate the passenger discomfort that was associated with earlier tilt train systems.
If Australia were to adopt a tilt train standard of D=180mm and I=300mm, this would allow a minimum radius of 983m at the design speed of 200km/h. Although this is a relatively aggressive tilt, it is the same as that used by both the UK and Germany. Modern tilt systems which anticipate curves in the track automatically are able to almost completely eliminate the passenger discomfort that was associated with earlier tilt train systems.
For this reason, Hot Rails will adopt an exceptional minimum curve radius of 1000m, and a typical minimum of 1500m (for permissible speeds of 200km/h and 250km/h respectively). With an eye to potential future speed upgrades, a desirable curve radius of 3000m will be adopted where practical to do so, which allows a TGV-style train to achieve 300km/h. However, upgrades to faster speed are contrary to the design philosophy of Hot Rails, which seeks to minimise capital costs by re-using existing alignment.
Transition curves
Railway tracks do not transition instantly from straight track to constant radius curvature. In order to limit the lateral jerk to acceptable levels, they employ a transition curve, typically a Euler Spiral in which the radius varies linearly along the length of the curve.
The length of the transition curve is also determined by the rate of change of cant – obviously, the outer rail must be raised gradually rather than suddenly. This is called a superelevation ramp, and it coincides with the transition curve. This is particularly the case for tilting trains, which must have a greater roll velocity due to their greater cant deficiency.
Australian XPT standards limit the rate of change of cant (dD/dt) to 65mm/s (exceptional value), or 55mm/s (typical). This implies that a superelevation ramp from D=0 to D=180mm would have to exceed 2.77 seconds in duration and 155m in length (assuming a speed of 200km/h). However this is quite conservative by world standards. UK standards for rate of change of cant deficiency (dI/dt) specify a maximum of 150mm/s. For maximum I of 300mm, this would require a transition curve exceeding 110m. Note that UK standards for dD/dt are higher than Australian standards, at 95mm/s for tilting trains. Therefore a transition curve length, LH,trans , of 150m is considered a conservative estimate sufficient for preliminary design purposes. For ease of plotting the preliminary alignment, the transition curves will be approximated by straight sections; this is acceptable due to LH,trans being small in comparison to R.
Vertical alignment
Vertical alignment refers to the slope or grade of the railway, the rate of change of slope, and the vertical radius of crests and troughs.
Grade
AECOM13 Appendix 2B specifies a desirable gradient of 1.25% or below, a typical maximum 0f 2.5%, and an exceptional maximum of 3.5%. ARUP01 goes into more detail, providing a graph of the maximum speed vs grade for various rollingstock including existing Australian intercity trains, tilting trains and maglevs. For most rollingstock, maximum speed begins to be severely limited at grades beyond 2%; only maglev technology can handle higher gradients with minimal performance penalty (GMGL = German MaGLev, referring to Transrapid technology by ThyssenKrupp).
Hot Rails proposes a less powerful trainset than TGV, probably with a maximum speed of 250km/h similar to the XNEC or AIM2 trains (XNEC was a proposed 250km/h version of the Swedish X2000, and AIM2 was a similar system proposed by Adtranz in the 1990s for a Sydney-Canberra HSR line). The graph shows that these trains are still capable of exceeding 200km/h at a gradient of 2%. For this reason, Hot Rails will adopt a more conservative gradient than AECOM13, with 1.25% desirable, 2% typical maximum, and 3% exceptional maximum.
Vertical radius
Vertical curve radii (RV) for high speed operation can be extremely large; Specifications from AECOM13 (for very high speed), ARUP01 (for high speed) and the ARTC (for lower speeds) are given below:
[table]
Maximum Train Speed,Recommended Limit,Typical Limit
80km/h,1300m,1800m
80-99km/h,2000m,3200m
100-119km/h,2800m,5000m
120-160km/h,5000m,7200m
200km/h,N/A,15450m
300km/h,N/A,25000m
400km/h,N/A,61730m
[/table]
Hot Rails will adopt a desirable RV of 25,000m (to allow for potential future speed upgrade), with a typical limit of 15,000m, and exceptional limit of 10,000m.
For preliminary design, it is far easier to convert these vertical curve radii to “transition lengths”, ie, the length of track required to transition from one grade to another. This can be calculated using the following formula, where LV,trans is the length of vertical transition curve, and Δθ is the change of gradient.
![]()
This is shown graphically below for the three values chosen for RV; a typical vertical transition curve from flat to 2° should be at least 500m in length.
NOTE: Vertical curves should not coincide with horizontal transitions.






Information is very important and can be used to estimate the implementation of railway projects