Underground transport infrastructure is extremely expensive, and usually comprises the bulk of expense for any high-speed railway through mountainous or rolling terrain. Nevertheless, there is reason to believe the estimate of $75 million per bore-kilometre used in AECOM13 is excessively high. In this post we will look at a range of Australian and international sources to arrive at a cost for tunnel construction with greater confidence.
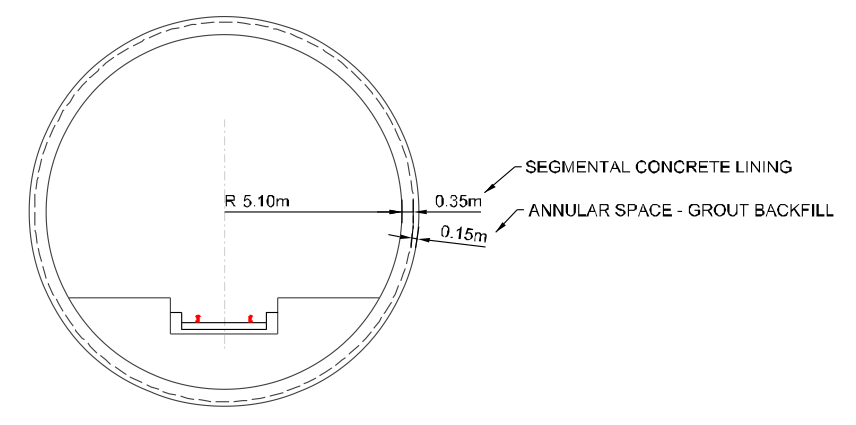
Typical tunnel section from AECOM13 study. Appendix 2B, pp17. Anybody else think you could fit three trains through there?
Tunnelling methods
In modern infrastructure projects, two types of tunnelling are usually used:
•Cut and Cover – large trenches are dug by conventional earthmoving equipment, then the “tunnel” is built within the trench, usually of pre-cast concrete sections. The tunnel is then covered by earth or paving over the top. It is only possible for shallow tunnels. Typical depths are 8 to 12 metres below grade, although depths of up to 20m are not uncommon. The “immersed tube” system for underwater tunnels is similar, involving pre-cast sections laid on the ocean floor, waterproof membrane applied, and then pumped dry.
Cut and Cover tunnelling process. Source: http://www.fhwa.dot.gov/bridge/tunnel/pubs/nhi09010/05.cfm
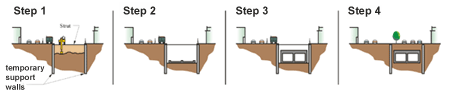
The “Stacked cut-and-cover” method is similar, but with the tracks placed one above the other to minimise the width of excavation. This is useful in situations where there is limited room available for excavation, such as under city streets where it is desired to keep the street partially open during construction.

Stacked cut-and-cover method, showing how roads can remain open during tunnel construction. Image: Canada Line
•Deep Bore – For deep tunnels, cylindrical Tunnel Boring Machines are used to bore directly into the earth; there is no limit to either the depth or length of tunnel (although ventilation may place a practical limit on length). Typical depth is greater than two diameters below the surface, and practical diameters range from 1 to 20 metres. TBMs are also sometimes used for shallow tunnels, if the cost of demolishing existing development makes the cut-and-cover technique prohibitively expensive. TBMs have largely replaced the older “drill and blast” technique.
A 2012 survey by the Worcester Polytechnic Institute for AECOM aimed to quantify the cost of tunnelling projects in Australia compared to the rest of the world. It found a very wide range of tunnel costs in different regions. In 2011 Australian Dollars per linear metre of “typical” road or rail tunnel, they were:
- China: $22,695
- New Zealand: $43,413
- USA: $50,744
- Australia: $59,809
- Italy: $88,451
- UK: $135,063
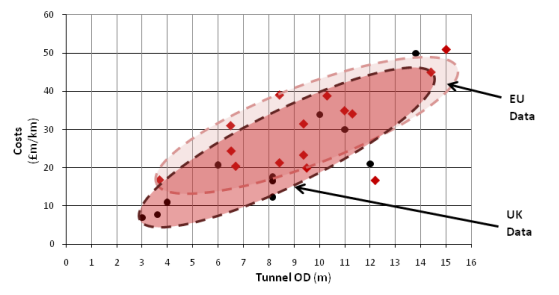
A 2010 report by the UK Government presented data for tunnel cost versus tunnel diameter, obtained from European sources and the British Tunnelling Society. The data follows an approximately linear trend, with visually estimated equation: Cost(million pounds per km) = 3.33*D (where diameter D is in metres). Assuming an exchange rate of 1.65£/AUD for 2010, this is about: Cost (million AUD per km) = 5.5*D. The same study also found a slightly negative trend for tunnel unit cost versus total length (although this did not consider tunnels shorter than 500m, which have lower safety, egress and ventilation requirements and are therefore cheaper).
Required tunnel dimensions and implied costs
High-speed rail requires a substantially larger tunnel size than normal rail due to aerodynamic considerations – the faster the design speed, the larger the cross-section required. AECOM13 provides a table of required tunnel dimensions for various design speeds. Note that these are internal diameters; AECOM13 assumes the lining thickness is 0.5m, thus OD will be 1m greater than indicated in the table below.
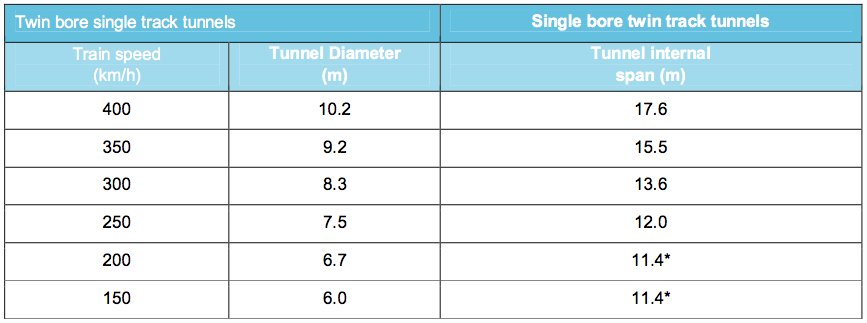
Required tunnel sizes (ID), * denotes minimum width due to size of trains. From AECOM13, Appendix 2B page 16
The UK Government report shows that the cost of tunnelling is strongly dependent on the outer diameter (OD) of the tunnel. In the Australian context, it may be preferable to use a dual-track tunnel, as service frequencies are likely to be low enough that trains passing each-other within the tunnel will be unlikely. Therefore, the larger cross-sectional area of dual-tunnel may be preferable to two smaller bores.
Using AECOM13’s diameter requirements, but the UK Government’s cost assumptions, we can estimate the tunnel cost, in million dollars per kilometre, for different design speeds.
Single track, dual bore (per bore):
- 150km/h: 38.5
- 200km/h: 42.4
- 250km/h: 46.8
- 300km/h: 51.2
- 350km/h: 56.1
- 400km/h: 61.6
Dual track, single bore:
- 150km/h: 68.2
- 200km/h: 68.2
- 250km/h: 71.5
- 300km/h: 80.3
- 350km/h: 90.8
- 400km/h: 101.8
So AECOM13’s assumption of $75m/track-km was a little high, but only by about 25%, and the WPI report was almost bang-on with $59.8m/km. It also agrees well with the estimates from the VFT study of 1989, which ranged from $24m to $40m/km ($45m to $75m in 2013 dollars), though this was for dual track. If we halve AECOM13’s excessive $27.7m/km “mark-up” cost (see justification here), we arrive at about the same number as WPI and the UK government, so the numbers presented above can be treated as high-confidence.
If we look simply at the tunnel itself, and eliminate track, overhead line, and signalling/comms, the cost drops by a further $5-6m/km. Short tunnels (<500m) do not require ventilation, fire protection or sophisticated lighting, resulting in a further $2m/km saving. Additionally, it is clear that the choice to adopt a design speed of 400km/h has greatly increased the required tunnel dimensions, and therefore the assumed cost of tunnelling. Reducing the design speed to a still-impressive 300km/h (allowing for substantial future upgrade from the Hot Rails assumption of 200km/h) will allow much more economical construction (a reduction of $10m/km for single track, or almost $22m/km for dual-track. Additionally, the assumptions for tunnel diameter may be generous; Austrian dual-track HSR tunnels are dug with an OD of 13m.
Cost for cut-and-cover tunnelling
It’s difficult to find much data on this; it’s so variable due to a whole lot of factors, not least of which is that you still have to disturb so much infrastructure on the surface when using this method. Proponents of deep-bore tunnelling claim that in many cases, cut and cover is actually more expensive (see e.g. this study by proponents of the New Austrian Tunnelling Method). However, there is evidence to suggest that, other things being equal, cut-and-cover is substantially cheaper than deep-bore. A study of various options for German metro construction found that cut-and-cover was typically about 30 to 45% cheaper than deep-bore methods.
Hot Rails will assume that cut-and-cover tunnelling costs 67% of a deep-bore tunnel designed for equivalent speed.
Conclusion
This investigation does not discredit the AECOM study’s cost estimates, but it does highlight the danger of overspecification. The cost difference between a tunnel specified for 300km/h (the top speed of almost every HSR system in the world today) and one specified for 400km/h (which is not currently achieved in regular service anywhere in the world) is about $20 million per kilometre, for a “future-proofing” feature that may never be used, and the extra costs of which jeopardise the whole project.
Hot Rails will adopt a design speed of 300km/h, single-bore/dual-track. This gives a cross-sectional area greater than for 400km/h single-track tunnels, and thus is considered sufficient for higher speeds as long as low service frequencies (say, 4 per hour in either direction) allow scheduling to prevent simultaneous tunnel use. As noted above, this is the same configuration and tunnel size as used in the Austrian high-speed rail system.
Additionally, we will exclude track-specific costs (rails, slab, overhead line and signalling/comms, totalling $6m per track-km) – these will be calculated independently. AECOM13 design dimensions will be used, with UK government cost estimates. This is considered to give substantial built-in contingency, given that the UK has been at the high end of worldwide construction cost experience. Additionally, the “mark-up” cost of AECOM13 remains, but halved to a more reasonable $13m/km (18% rather than 36% of the total cost). The difference between short tunnels (<500m) and longer ones is not significant (~$2m/km), so they will not be treated differently.
- Single track (per bore)
- 7.7m bore diameter
- $42.4m/km, less ~$6m/km
- = $36m/km
- Dual Track
- 12.4m bore diameter
- $68.2m/km, less ~$6m/km
- = $62m/km
If you think I’m crazy to specify the tunnels to only 200km/h, or are doubtful that higher speeds will be safely achievable without larger diameter tunnels, apply the following cost multipliers according to your desired design speed:
- 250km/h: 1.05
- 300km/h: 1.175
- 350km/h: 1.33
- 400km/h: 1.50




What would have been the cost of a cut and cover tunnel for the Canberra light rail along the section from Epic to Civic?
That’s about 6km, dual track, low speed, so call it maybe $45m/km, or $275m in total. Probably not worth it given the wide median strip making an excellent tram corridor. You’d still get all the disadvantage of disrupting traffic and underground services during construction as well. Much as I’m happy that Canberra light rail has been built, it was already plenty expensive without putting it underground.